Methods of solving system of the linear equations: Definition, explanation, & calculations

Methods of solving system of the linear equations: Definition, explanation, & calculations

In algebra, the system of linear equations is referred to as a set of two or more linear equations with at least two variables of degree one. Linear equations are those equations in which the power of each variable is one.

The constant coefficients are involved in the linear equations as the product of the variable. The linear equations are:

2x + 5y = 9

4x + 12y = 16

In this article, we will learn the methods for solving the system of linear equations with examples.

Graphing method

What is the system of linear equations?

In algebra, a set of two or more first-degree equations (linear equations or one-degree equations) containing the same variables i.e., x & y, a & b, p & q, etc. is said to be the system of linear equations. 

The linear equation contains the polynomial of degree one such as the power of each variable in the equation must be one. The constant and the constant coefficients are also present in the linear equation and an equality sign. 

For example, the system of linear equations for p & q variables are:

2p + 3q = 12; 6p – 4q = 10

The above two linear equations are said to be the system of linear equations for 2 variables. The purpose of solving a system of linear equations is to find the values of unknown variables of the equations that must satisfy both equations simultaneously. 

In simple words, solving the system of linear equation is the process of finding variables that makes both equations true at the same time. The results of the system of linear equations must be different in different scenarios. The solution set of the system of linear equations is (x, y) and the solution set can’t satisfy the inconsistent equations.

Methods for solving the system of linear equations

There are different methods for solving the system of linear equations. We’ll discuss some of the methods of solving linear equations that are frequently used.

Elimination method

The system of linear equations is solved through the elimination method as a well-defined technique. According to this technique, the process of addition and subtraction is performed on linear equations to eliminate one variable.

Then the other variable is solved simultaneously to take the numerical value. After that, the calculated variable is to be substituted into any equation to get the result of the eliminated variable. 

This method can be used as taking a similar variable to cancel them such as if a variable “p” in both equations is the same with the same signs, then we have to subtract the equations simultaneously. And if the coefficients are variable are same with opposite signs then you have to add the equations simultaneously.  

If the equations don’t have any similar coefficients, then multiply one or both equations with a suitable integer to make the same coefficients of one variable.  

Examples of elimination method 

The elimination method is a well-known technique for solving the system of linear equations to find the values of unknowns. Here are a few examples.

Example 1

Evaluate the values of unknown variables of a given system of linear equations.  

2p – 4q = 4

3p + q = 6

Solution

Step 1: Multiply the second equation by 4 to make the same coefficients of “q”.

4* (3p + q) = 4 * 6

4* 3p + 4 * q = 4 * 6

12p + 4q = 24 

Step 2: The coefficients of “q” have opposite signs, so we have to add the equations simultaneously.

2p – 4q = 4

12p + 4q = 24 

 14p + 0q = 28

14p = 28

p = 28/14 = 14/7 = 2

Step 3: Now substitute the value of p to any equation to determine the value of eliminated variable “q”.

2(2) – 4q = 4

4 – 4q = 4

– 4q = 4 – 4

– 4q = 0

q = 0/-4

q = 0

hence the solution set of the given equation is (2, 0)

Online elimination method calculators will be a handy tool for determining the values of unknown variables of the system of linaer equation. Let us solve the above example through online tool.

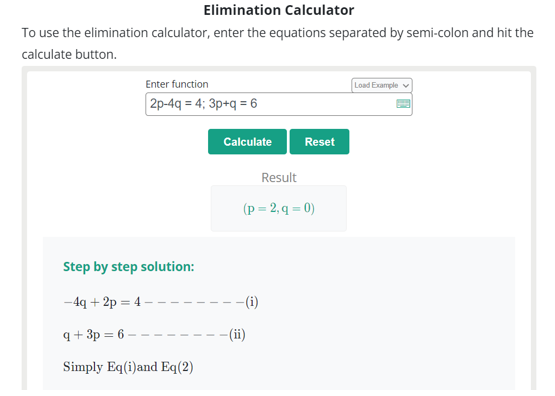
System of linear equations solved through (https://www.allmath.com/elimination-calculator.php)

Example 2

Evaluate the values of unknown variables of the given system of linear equations.

2p + 7q = 12

3p + 3q = 5

Solution

Step 1: Now multiply the first equation by 3 and the second equation by 2 to make the same coefficients of “p”.

3 (2p + 7q = 12) → 6p + 21q = 36

2 (3p + 3q = 5) → 6p + 6q = 10

Step 2: Now eliminate “p” by subtracting the linear equation simultaneously.

   6p + 21q = 36

-(6p + 6q = 10)

   0 + 15q = 26

15q = 26

q = 26/15

Step 3: Now substitute the value of q to any equation to determine the value of eliminated variable “p”.

3p + 3(26/15) = 5

3p + (26/5) = 5

3p = 5 * 5/26

3p = 25/26

p = 25/26 * 3

p = 25/78

hence the solution set of the given equation is (25/78, 26/15).

Substitution Method

The second and well-known method of solving a system of linear equations is the substitution method. In this technique, we have to find the value of the first unknown variable and substitute it with the other linear equation to find the value of unknowns.

In other words, the basics of this technique are to reduce one linear equation in the form of one variable and put it in the other equation. It will make the equation for one variable and the other variable will be removed. After finding the unknown, put it into the first reduce form to find the other variable. 

Examples of Substitution Methods

The substitution method is a 2nd well-known technique for solving the system of linear equations to find the values of unknowns. Here are a few examples. 

Example 1

Find the values of unknowns by solving the given system of linear equations simultaneously. 

4p + 2q = 14

16p + 8q = 24

Solution

Step 1: Take the given system of linear equations

4p + 2q = 14

6p + 8q = 24

Step 2: Now reduce the first equation to make the equation for “q”.

4p + 2q = 14

2q = 14 – 4p

q = [14 – 4p] / 2

q = 14/2 – 4p/ 2

q = 7 – 2p

Step 3: Now place the value of “q” into the second linear equation. 

6p + 8q = 24

6p + 8(7 – 2p) = 24

6p + 56 – 16p = 24

56 – 10p = 24

– 10p = 24 – 56 

– 10p = – 32 

10p = 32 

p = 32/10 

p = 3.2

Step 4: Now place the value of p in the reduced form of the first equation. 

q = 7 – 2 (3.2)

q = 7 – 6.4

q = 0.6

q = 6/10

Hence the solution set of a system of linear equations is (3.2, 0.6).

Example 2

Find the values of unknowns by solving the given system of linear equations simultaneously. 

p – 4q = 5

4p + 12q = 12

Solution

Step 1: Take the given system of linear equations

p – 4q = 5

4p + 12q = 12

Step 2: Now reduce the first equation to make the equation for “q”.

p – 4q = 5

p = 5 + 4q

Step 3: Now place the value of “q” into the second linear equation. 

4p + 12q = 12

4(5 + 4q) + 12q = 12

4 * 5 + 4 * 4q + 12q = 12

20 + 16q + 12q = 12

20 + 28q = 12

28q = 12 – 20

28q = -8

q = -8/28

q = -4/14 = -2/7

Step 4: Now place the value of p in the reduced form of the first equation. 

p = 5 + 4(-2/7)

p = 5 – 4(2/7)

p = 5 – 8/7

p = (35 – 8)/7

p = 27/7

Hence the solution set of the system of linear equations is (27/7, -2/7).

Summary

The system of linear equations plays a vital role in algebra to evaluate the values of unknown variables of the linear equation which satisfies them. the elimination and substitution methods are two well-known techniques for solving the system of linear equations.