प्रदत्तों के आरेखीय चित्रण से आप क्या समझते हैं?

Contents

प्रदत्तों के आरेखीय चित्रण से आप क्या समझते हैं? What do you understand by diagrammatic representation of data?

विभिन्न अध्ययनों से प्राप्त समंकों को जनसाधारण तक पहुँचाना आवश्यक होता है जैसे शिक्षा के विभिन्न स्तरों पर बालक बालिकाओं की संख्या देश में साक्षरता की स्थिति, परीक्षा में छात्रों की सफलता का प्रतिशत आदि। इन समंकों को स्पष्ट करने के लिये रेखाचित्रों का प्रयोग किया जाता है। इनसे न केवल अध्ययन से प्राप्त प्रदत्तों को समझने में सहायता मिलती है वरन् विश्लेषण व निष्कर्ष निकालने में भी सहायता मिलती है। विभिन्न सांख्यिकीय प्रदत्तों को ग्राफ पेपर पर प्रदर्शित करने को रेखाचित्र (Graph) कहा जाता है।

रेखाचित्रण के सामान्य सिद्धान्त

1. रेखाचित्रण ग्राफ पेपर के मध्य में बनाया जाता है एवं कुछ स्थान खाली छोड़ दिया जाता है जहाँ आवश्यक विवरण अंकित किया जाता है।

2. रेखाचित्र पैमाने (Scale) के अनुसार बनाना चाहिये।

3. किसी भी समंक के लिये वही रेखाचित्र बनाना चाहिये जो उसे सर्वाधिक रूप से स्पष्ट कर सके। रेखाचित्र को नामांकित करना चाहिये ।

4. रेखाचित्रण दो भुजाओं के आधार पर किया जाता है। क्षैतिज रेखा जिसे एक्स अक्ष कहा जाता है तथा लम्बवत् रेखा जिसे वाई अक्ष कहा जाता है। जिस बिन्दु पर ये दोनों भुजाएँ मिलती हैं उसे मूल बिन्दु (Point of Origin) कहा जाता है जिसे शून्य से व्यक्त करते हैं ।

5. एक्स अक्ष (X-axis) वाई अक्ष (Y-axis) से अधिक बड़ा होता है। इनका अनुपात 4:3 का होना चाहिये। यदि x अक्ष की लम्बाई 4 इंच है, तो y अक्ष की लम्बाई 3 इंच होनी चाहिये।

आरेखीचित्रों के प्रकार

रेखाचित्रों के प्रमुख प्रकार निम्नलिखित हैं-

1. स्तम्भ रेखाचित्र (Bar Diagram) – सांख्यिकीय के प्राप्त समंकों को जब ग्राफ पर खड़े रूप में प्रकट करते हैं तो इसे दण्ड आरेख या स्तम्भ रेखाचित्र कहते हैं। यह दण्ड आरेख अधिकांशतया शिक्षकों, स्कूलों व छात्रों की संख्या तथा शिक्षित-अशिक्षितों की संख्या को प्रकट करने के लिए करते हैं। इसके द्वारा दो या दो से ज्यादा समूहों की मध्य भाग को योग्यता को स्पष्ट करते हैं वैसे तो इसे क्षैतिज व लम्बवत् किसी भी दिशा में निर्मित किया जा सकता है किन्तु इन्हें अधिकतर लम्बवत् ही बनाते हैं। दण्ड आरेखों को निम्न प्रकार की रेखाओं एवं रंगों से ज्यादा आकर्षक लगता है।

2. वृत्त चित्र (Circle or Pie Diagram) – जब सांख्यिकीय के समंकों को वृत्त में रेखांकित किया जाता है तो इसे वृत्त आरेख कहा जाता है; वृत्त का केन्द्र बिन्दु आरेख केन्द्र बिन्दु कहलाता है। वृत्त आरेख के निर्माण का पैमाना कोणों में होते हैं। इस तरह के आरेख को दोलीय

आरेख भी कहते हैं। इसका प्रयोग किसी पूर्ण संख्या को अलग-अलग हिस्सों में दर्शाने के लिए किया जाता है। इसमें विभिन्न प्रकार के रंगों का प्रयोग होने से वृत्त आकर्षक एवं स्पष्ट होते हैं।

3. आवृत्ति बहुभुज (Frequency Polygon)- जब आवृत्ति वितरण को दण्डों की शीर्ष रेखाओं के बीच बिन्दुओं को मिलाकर दर्शाते हैं तो इस प्रकार से निर्मित किये गये बहुभुज आकृति को आवृत्ति बहुभुज कहा जाता है। वर्गों की संख्या जब ज्यादा होती है तो उन्हें स्तम्भों की जगह रेखाओं के माध्यम से प्रदर्शित करते हैं। इसे निर्मित करने के लिए सबसे निम्न और सबसे उच्च एक-एक वर्ग को जोड़ लिया जाता है तथा इसकी आवृत्ति को शून्य माना जाता है। इसके बाद प्रत्येक वर्ग की पूरी आवृत्तियों को उनके मध्य बिन्दुओं पर केन्द्रित मानकर इन बिन्दुओं को चिन्हित किया जाता है इसके पश्चात बिन्दुओं को क्रमश: सीधी रेखाओं से जोड़ दिया जाता है। इस तरह प्राप्त बहुभुज आकृति को आवृत्ति बहुभुज कहते हैं।

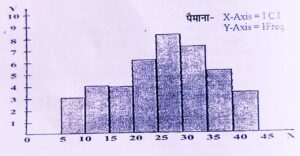
4. स्तम्भाकृति, आयत चित्र (Histogram) – जब सांख्यिकीय के समंकों को जब दण्ड आरेख के रूप में प्रस्तुत किया जाता है तो उसे आवृत्ति दण्डाकृति कहा जाता है। दण्डाकृति में प्राप्तांक वर्गों को अक्ष रेखा पर एवं आवृत्तियों को उदग्र रेखा पर दर्शाते हैं। इसके पैमाने कई मानने में कुछ सावधानियों को अपनाया जाता है। ग्राफ पेपर के केन्द्रीय बिन्दु o पर दिए गये आंकड़ों के पहले के आंकड़े लिखे जाते हैं जिसके द्वारा आरेख निर्मित करने में आसानी होती है।

उदाहरण- 50 अंकों की एक गणित परीक्षा में 40 छात्रों के प्राप्तांकों की आवृत्ति वितरण तालिका नीचे दी गई है। इसे आवृत्ति दण्डाकृति द्वारा स्पष्ट कीजिए।

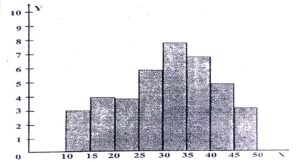
5. संचित आवृत्ति वक्र (Cumulative Frequency Curve)- जब आवृत्ति बहुभुज के शीर्ष बिन्दुओं को सीधी रेखों से न जोड़कर गोलाई में जोड़ते हैं तो इस तरह से निर्मित आकृति को आवृत्ति वक्र कहा जाता है।

रचना विधि- ठीक उसी प्रकार जिस प्रकार आवृत्ति बहुभुज तैयार किया गया है, बस वर्ग विशेष की आवृत्तियों के केन्द्र बिन्दुओं को सीधी रेखाओं से जोड़ने के स्थान पर उन्हें फी हैण्ड द्वारा गोलाई में जोड़ा जाता है।

IMPORTANT LINK

Disclaimer: Target Notes does not own this book, PDF Materials Images, neither created nor scanned. We just provide the Images and PDF links already available on the internet. If any way it violates the law or has any issues then kindly mail us: targetnotes1@gmail.com